Chapter 64: Exterior Algebra

This chapter is based on a GDC talk called “Fundamentals of Grassman Algebra” by Eric Lengyel.

Exterior Algebra is the basis for the geometric algebra we use in computer graphics. By understanding these fundamentals, we will understand:

Where the cross product comes from and why it behaves the way it does
Where the dot product comes from

Clifford Algebras

The Clifford Algebras describe a set of algebras extending the real numbers. In this context, we’re discussing “an algebra” which refers to something like a number system - a mathematic structure that includes some sort of number and a multiplication operation between them. This is different from the general term “algebra” which describes math involving variables.

In n dimensions, take the real numbers and add n special units $e_1, e_2, \ldots, e_n$ Then, choose whether each $e_i$ squares to 0, 1, or -1.

Complex Numbers are an example of a Clifford Algebra - specifically, the one dimensional numbers with a single unit $e$ , usually called $i$ , that squares to $-1$ . Another example that comes up the Dual Numbers, one dimensional numbers where $e$ squares to 0.

Grassman Algebra or Exterior Algebra is an n dimensional algebra where all $n$ of the $e_i$ square to 0.

The Wedge Product

Also known as the progressive product or the exterior product, the wedge product is the basis for a lot of the math we do in 3D computer graphcs.

$a \wedge b$

The wedge product operates on scalars, vectors, and more. Operations involving scalars should be very familiar:

$s \wedge t = t \wedge s = st$ $s \wedge \vec v = \vec v \wedge s = s \vec v$

The first interesting part of the wedge product is that a vector wedged with itself is 0.

$\vec v \wedge \vec v = 0$

This leads to what’s called anti-commutivity for this operation on vectors.

$(\vec a + \vec b) \wedge (\vec a + \vec b) = 0$ $\vec a \wedge \vec a + \vec a \wedge \vec b + \vec b \wedge \vec a + \vec b \wedge \vec b = 0$ $\vec a \wedge \vec b + \vec b \wedge \vec a = 0$ $\vec a \wedge \vec b = - \vec b \wedge \vec a$

Bivectors

Another property of the wedge product is that the product of two vectors is not a vector - it is something else, specifically a bivector. Bivectors are distinct from scalars and vectors, and represents an oriented 2D area (whereas a vector represents an oriented 1D direction and scalars are zero-dimensional values).

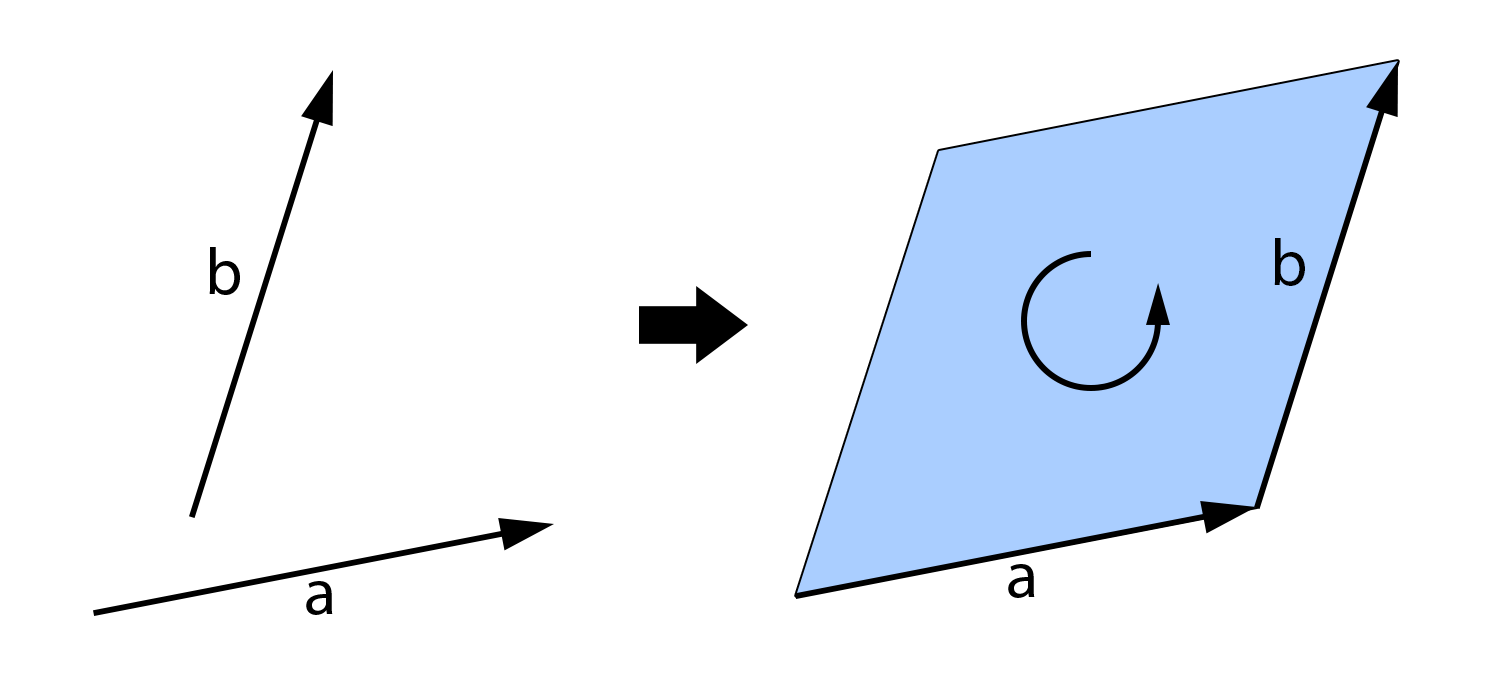
The orientation of this area is sometimes called the “winding” and can be described as clockwise or counterclockwise. This also illustrates the anticommutivity of the wedge product - changing the order of operands reverses the orientation of the bivector.

Bivectors in 3D

Start with 3 orthonormal basis vectors $e_1, e_2, e_3$ . Then, a 3D vector $\vec a$ can be expressed as

$a_1 e_1 + a_2 e_2 + a_3 e_3$

from this we can see that:

$a \wedge b = (a_1 e_1 + a_2 e_2 + a_3 e_3) \wedge (b_1 e_1 + b_2 e_2 + b_3 e_3)$

Multiply through and cancel out every $e_i$ product with itself:

$a \wedge b = a_1 b_2 (e_1 \wedge e_2) + a_1 b_3 (e_1 \wedge e_3) + a_2 b_1 (e_2 \wedge e_1) +$ $a_2 b_3 (e_2 \wedge e_3) + a_3 b_1 (e_3 \wedge e_1) + a_3 b_2 (e_3 \wedge e_2)$

Then group parts with the same wedge products:

$a \wedge b = (a_2 b_3 - a_3 b_2) (e_2 \wedge e_3) +$ $(a_3 b_1 - a_1 b_3) (e_3 \wedge e_1) +$ $(a_1 b_2 - a_2 b_1) (e_1 \wedge e_2)$

These three bivectors, $(e_2 \wedge e_3)$ , $(e_1 \wedge e_3)$ , and $(e_1 \wedge e_2)$ , form the basis for any bivector. That is, any bivector can be written as a linear combination of these three bivectors.

This is a little unwieldy to write so we use shorthand notation for these bivectors:

$e_{12} = e_1 \wedge e_2$ $e_{23} = e_2 \wedge e_3$ $e_{31} = e_3 \wedge e_1$ $e_{123} = e_1 \wedge e_2 \wedge e_3$

Using that same notation we can write out the wedge product a little more compactly:

$a \wedge b = (a_2 b_3 - a_3 b_2) e_{23} + (a_3 b_1 - a_1 b_3) e_{31} + (a_1 b_2 - a_2 b_1) e_{12}$

This looks quite a bit similar to the cross product, but it is a bit more than a cross product. The cross product is only defined in 3D, and is not associative.

$(\vec a \times \vec b) \times \vec c \neq \vec a \times (\vec b \times \vec c)$

Conversely, the wedge product is both associate and defined in all dimensions. This comes from the fact that the wedge between two vectors is not a vector - it’s a bivector.

Trivectors

Similarly, the wedge product of three vectors produces a trivector. Trivectors represent a 3D oriented volume.

$\vec a \wedge \vec b \wedge \vec c$

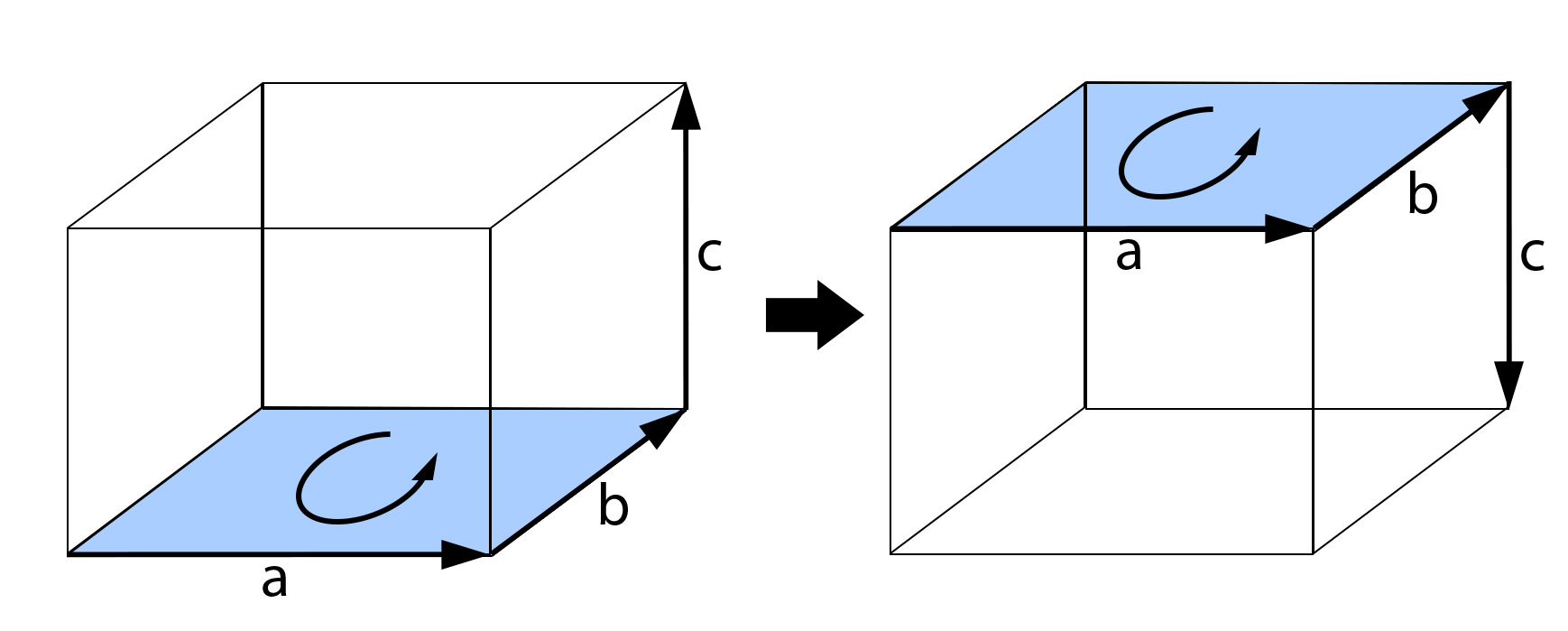
If one of the vectors is reversed, the opposite (negated) volume is produced.

A 3D trivector only has one component:

$\vec a \wedge \vec b \wedge \vec c =$ $(a_1 b_2 c_3 + a_2 b_3 c_1 + a_3 b_1 c_2 - a_1 b_3 c_2 - a_2 b_1 c_3 - a_3 b_2 c_1) e_{123}$

And the magnitude is:

$\text{det} \begin{bmatrix} \vec a & \vec b & \vec c \\ \end{bmatrix}$

(This is where the determinant comes from - it is derived from exterior algebra).

Because a trivector is a simple component, it looks a lot like a scalar. As such it is also called an antiscalar. It transforms differently than scalars though - it will negate under reflection.

Trivectors are the end for 3D. If we try to throw another vector into the mix, we’ll just get zero.

$\vec a \wedge \vec b \wedge \vec c \wedge \vec d = 0$

This is because we’ll always have a duplicated term in each part of the product, e.g. $e_1 \wedge e_1$ , which of course is zero.

Entities

All of these entities in exterior algebra have a grade, which is really just “how many vectors were wedged to get this?”

Scalars have grade 0
Vectors have grade 1
Bivectors have grade 2
Trivectors have grade 3
etc.

In 3D algebra, we can’t get higher than trivectors. In any n dimensional exterior algebra, you can’t have entities with grade greater than n.

Each entity in the algebra has a number of elements, or components, as we have seen:

1 scalar element
3 vector elements
3 bivector elements
1 trivector element

The fact that vectors and bivectors have the same number of elements is one of the reasons we don’t usually hear about bivectors - they look so similar to vectors.

In four dimensions, we have four basis vectors $e_1, e_2, e_3, e_4$ , and a fifth entitiy - quadvectors (with grade 4).

However, the elements follow a different pattern:

1 scalar element
4 vector elements
6 bivector elements
4 trivector elements
1 quadvector element

In general, the number of elements for each grade follows Pascal’s triangle.

        1   1
 2   1
 3   3   1
 4   6   4   1
 5  10   10  5   1

The symmetric nature of this structure is important. For every n dimensional algebra, there are vector entities with n elements as well as a matching higher-grade entity with n elements as well. In 3D, this relationship exists between vectors and bivectors, so let’s take a closer look.

Antivectors and Antiscalars

As we mentioned, in 3D trivectors are somtimes called antiscalars due to them only having a single element.

Bivectors are similarily related to vectors, in that they both have three components, so they are sometimes called antivectors. Note how a vector has three elements each using exactly one of the spatial directions ( $e_1, e_2, e_3$ ). Comparatively, an antivector has three elements using all except one of the spatial directions ( $e_{23}, e_{31}, e_{12}$ ).

There’s a correspondance between these basis elements - e.g. the first vector element contains only $e_1$ while the first bivector element contains everything but $e_1$ . So, we use a notation that reflects this:

$\bar e_1 = e_2 \wedge e_3 = e_{23}$ $\bar e_2 = e_3 \wedge e_1 = e_{31}$ $\bar e_3 = e_1 \wedge e_2 = e_{12}$

The order here is specifically chosen such that:

$e_i \bar e_i = e_1 \wedge e_2 \wedge e_3$

in all cases (and with extension to any n dimensions).

The wedge product between a vector and an antivector is the dot product - and it produces an antiscalar.

$(a_1e_1 + a_2e_2 + a_3e_3) \wedge (b_1\bar e_1 + b_2\bar e_2 + b_3\bar e_3)$ $= (a_1b_1 + a_2b_2 + a_3b_3) (e_1 \wedge e_2 \wedge e_3)$

And this is what we do in shading - $N \cdot L$ - here $N$ is an antivector (or bivector).

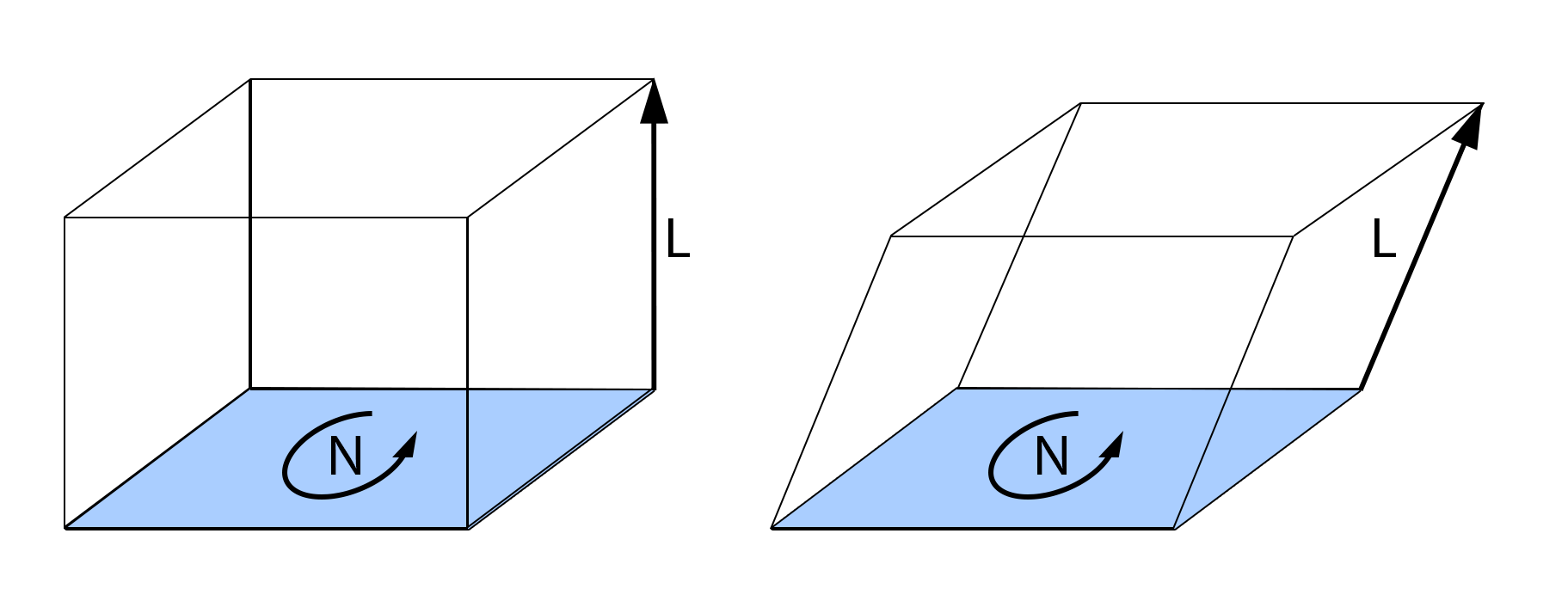
What are the consequences of this? Well, an antiscalar is different from a scalar in that it flips sign under certain transforms, such as a mirror transform. If you take a 3D model and mirror it, all of the faces will be pointing inwards and your shading will be reversed. Of course we know this will happen since mirroring the mesh will reverse the normals. However, we don’t need to “recompute” $N \cdot L$ to know that it will be flipped by this transformation, so long as we understand that it’s an antiscalar.

← Game Programming Patterns

↑ Theory ↑

Anti-Aliasing →